উপপাদ্য : অর্ধবৃত্তস্থ কোণ এক সমকোণ বা $90^{\circ}$
| History | 📡 Page Views |
|---|---|
|
Published 05-Dec-2025 | 02:09 AM |
Total View 53 |
|
Last Updated 04-Jan-2026 | 11:28 AM |
Today View 0 |
অর্ধবৃত্তস্থ কোণ এক সমকোণ বা $90^{\circ}$
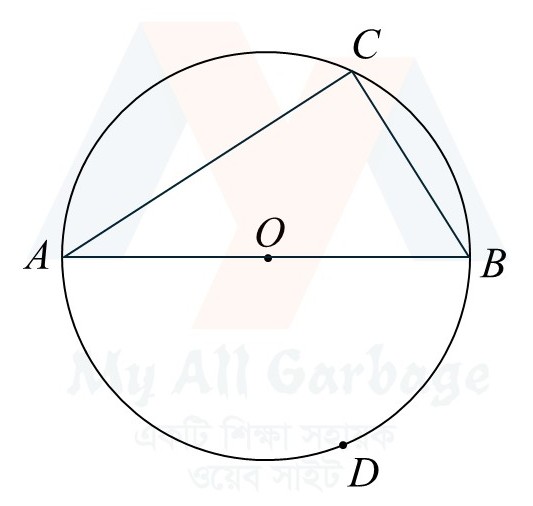
মনে করি, $O$ কেন্দ্রবিশিষ্ট বৃত্তে $AB$ একটি ব্যাস এবং $\angle ACB$ একটি অর্ধবৃত্তস্থ কোণ। প্রমাণ করতে হবে যে, $\angle ACB$ এক সমকোণ বা $90^{\circ}$
অঙ্কন : $AB$ এর যে পাশে $C$ বিন্দু অবস্থিত, তার বিপরীত পাশে বৃত্তের উপর একটি বিন্দু $D$ নিই।
প্রমাণ :
ধাপ ১ : $ADB$ চাপের ওপর দণ্ডায়মান
বৃত্তস্থ $\angle ACB =\frac{1}{2}$ (কেন্দ্রস্থ সরল কোণ $\angle AOB$) [$\because$ একই চাপের ওপর দণ্ডায়মাণ বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক]
ধাপ ২ : কিন্তু সরলকোণ $\angle AOB=$ দুই সমকোণ বা $2$ সমকোণ
$\angle ACB=\frac{1}{2} \cdot 2$ সমকোণ
বা, $\angle ACB=1$ সমকোণ।
$\therefore \angle ACB=90^{\circ}$ (প্রমাণিত)

Leave a Comment (Text or Voice)
Comments (0)