উপপাদ্য : দুইটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করলে, এদের কেন্দ্রদ্বয় ও স্পর্শ বিন্দু সমরেখ।
| History | 📡 Page Views |
|---|---|
|
Published 28-Nov-2025 | 07:08 PM |
Total View 35 |
|
Last Updated 31-Dec-2025 | 07:41 PM |
Today View 0 |
দুইটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করলে, এদের কেন্দ্রদ্বয় ও স্পর্শ বিন্দু সমরেখ।
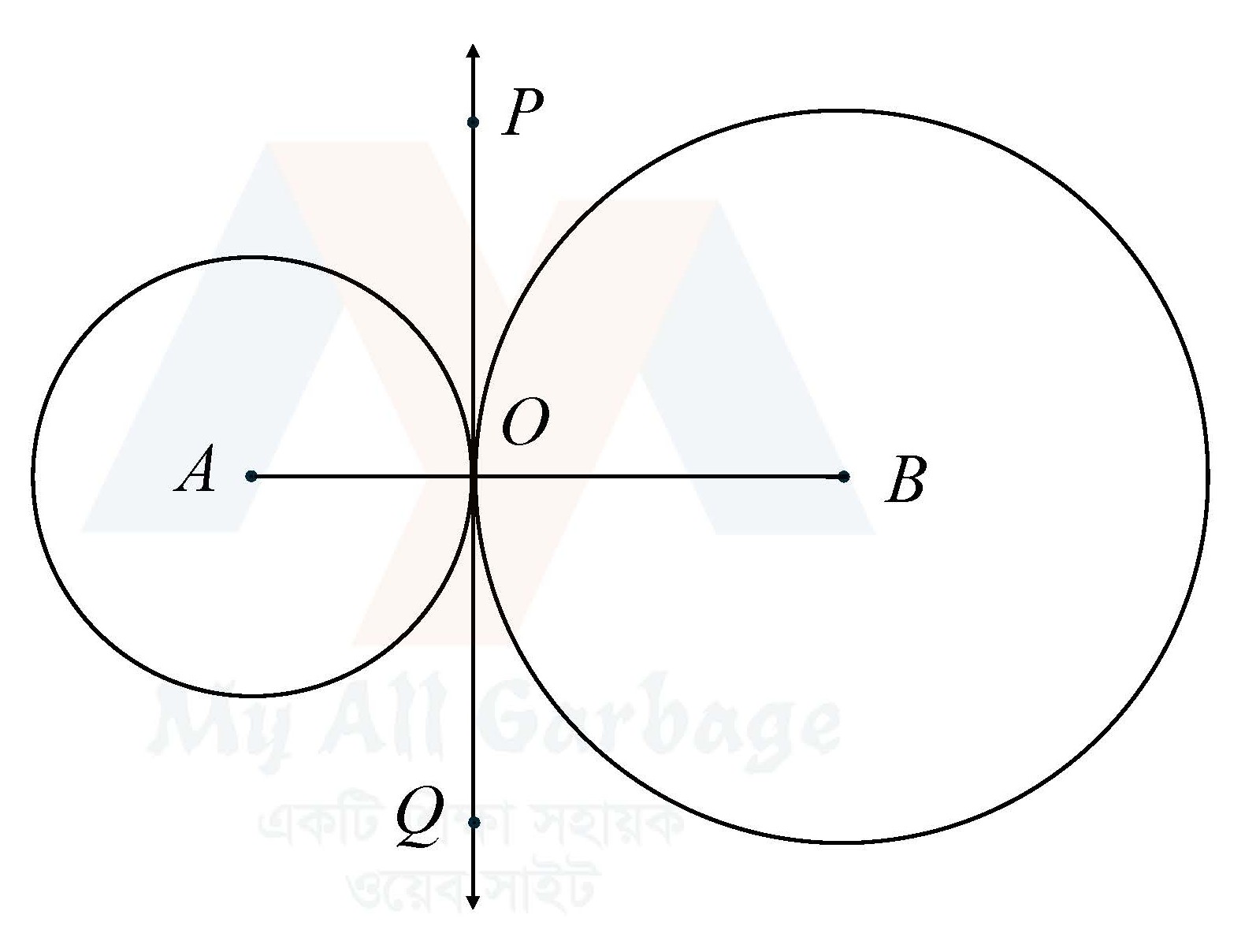
মনে করি, $A$ ও $B$ কেন্দ্রবিশিষ্ট দুইটি বৃত্ত পরস্পর $O$ বিন্দুতে বহিঃস্পর্শ করে। প্রমাণ করতে হবে যে, $A$, $O$, $B$ বিন্দু তিনটি সমরেখ।
অঙ্কন : যেহেতু বৃত্তদ্বয় পরস্পর $O$ বিন্দুতে স্পর্শ করেছে, সুতরাং $O$ বিন্দুতে এদের একটি সাধারণ স্পর্শক থাকবে। এখন $O$ বিন্দুতে সাধারণ স্পর্শক $POQ$ অঙ্কন করি এবং $O$, $A$ ও $O$, $B$ যোগ করি।
প্রমাণ : $A$ কেন্দ্রবিশিষ্ট বৃত্তে $OA$ স্পর্শবিন্দুগামী এবং $POQ$ স্পর্শক। সুতরাং $\angle POA =$ এক সমকোণ। তদ্রুপ $\angle POB=$ এক সমকোণ $\angle POA +\angle POB=$ এক সমকোণ $+$ এক সমকোণ $=$ দুই সমকোণ।
বা, $\angle AOB=$ দুই সমকোণ
অর্থাৎ, $\angle AOB$ একটি সরলকোণ।
$\therefore$ $A$, $O$, $B$ বিন্দুদ্বয় সমরেখ। (প্রমাণিত)

Leave a Comment (Text or Voice)
Comments (0)