উপপাদ্য : বৃত্তের যেকোনো বিন্দুতে অঙ্কিত স্পর্শক স্পর্শবিন্দুগামী ব্যাসার্ধের ওপর লম্ব।
| History | 📡 Page Views |
|---|---|
|
Published 28-Nov-2025 | 08:13 PM |
Total View 57 |
|
Last Updated 31-Dec-2025 | 07:41 PM |
Today View 1 |
বৃত্তের যেকোনো বিন্দুতে অঙ্কিত স্পর্শক স্পর্শবিন্দুগামী ব্যাসার্ধের ওপর লম্ব।
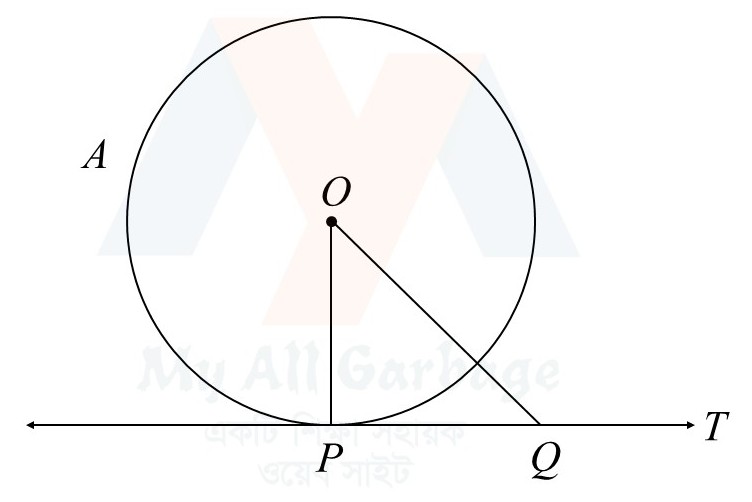
মনে করি, $O$ কেন্দ্রবিশিষ্ট একটি বৃত্তের ওপরস্থ $P$ বিন্দুতে $PT$ একটি স্পর্শক এবং $OP$ স্পর্শবিন্দুগামী ব্যাসার্ধ। প্রমাণ করতে হবে যে, $PT \perp OP$
অঙ্কন : $PT$ স্পর্শকের ওপর যেকোনো একটি বিন্দু $Q$ নিই এবং $O$, $Q$ যোগ করি।
প্রমাণ : যেহেতু বৃত্তের $P$ বিন্দুতে $PT$ একটি স্পর্শক, সুতরাং ঐ $P$ বিন্দু ব্যতীত $PT$ এর ওপরস্থ অন্য সকল বিন্দু বৃত্তের বাইরে থাকবে। সুতরাং $Q$ বিন্দুটি বৃত্তের বাইরে অবস্থিত।
$\therefore$ $OQ$ বৃত্তের ব্যাসার্ধ $OP$ এর চেয়ে বড়, অর্থাৎ, $OQ > OP$ এবং তা স্পর্শবিন্দু $P$ ব্যতীত $PT$ এর ওপরস্থ $Q$ বিন্দুর সকল অবস্থানের জন্য সত্য।
$\therefore$ কেন্দ্র $O$ থেকে $PT$ স্পর্শকের ওপর $OP$ হলো ক্ষুদ্রতম দূরত্ব।
সুতরাং $PT \perp OP$ [কোনো সরল রেখার বহিঃস্থ কোনো বিন্দু থেকে উক্ত সরল রেখার উপর যতগুলো রেখাংশ টানা যায় তন্মধ্যে লম্ব রেখাংশটিই ক্ষুদ্রতম] (প্রমাণিত)
⚡ Trending Posts
- মার্চ ১৯৭১ - প্রতিটি দিনের ঘটনা
- প্রবন্ধ রচনা : বাংলাদেশের গণহত্যা : ২৫শে মার্চ
- ৭ই মার্চ, ১৯৭১ : বঙ্গবন্ধুর ঐতিহাসিক ভাষণ - PDF - Audio
- প্রবন্ধ রচনা : ৭ মার্চের ঐতিহাসিক ভাষণের তাৎপর্য - PDF
- অনুচ্ছেদ : ৭ই মার্চের ঐতিহাসিক ভাষণ
- সাধারণ জ্ঞান : ৭ মার্চের ঐতিহাসিক ভাষণ / অপারেশন সার্চলাইট / স্বাধীন বাংলা বেতারকেন্দ্র
- গুরুত্বপূর্ণ দিবসগুলোর পোস্ট সমূহ
Leave a Comment (Text or Voice)
Comments (0)