উপপাদ্য : কোনো চতুর্ভুজের দুইটি বিপরীত কোণ সম্পূরক হলে তার শীর্ষবিন্দু চারটি সমবৃত্ত হয়।
| Article Stats | 📡 Page Views |
|---|---|
|
Reading Effort 153 words | 1 min to read |
Total View 97 |
|
Last Updated 31-Dec-2025 | 07:41 PM |
Today View 0 |
কোনো চতুর্ভুজের দুইটি বিপরীত কোণ সম্পূরক হলে তার শীর্ষবিন্দু চারটি সমবৃত্ত হয়।
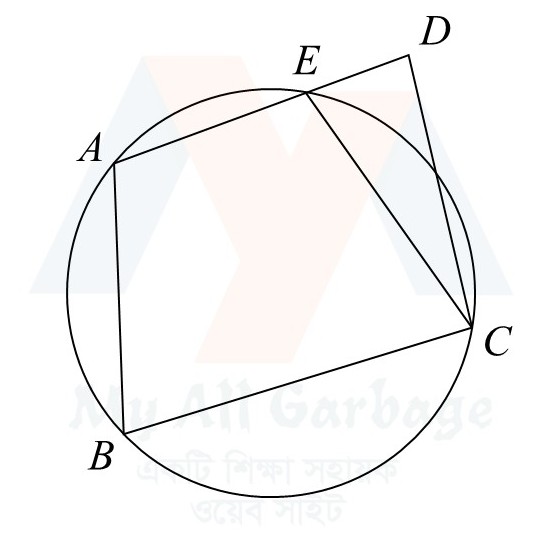
মনে করি, $ABCD$ চতুর্ভুজে $\angle ABC + \angle ADC =$ দুই সমকোণ। প্রমাণ করতে হবে যে, $A$, $B$, $C$, $D$ বিন্দু চারটি সমবৃত্ত।
অঙ্কন : যেহেতু $A$, $B$, $C$ বিন্দু তিনটি সমরেখ নয়, সুতরাং বিন্দু তিনটি দিয়ে যায় এরূপ একটি ও কেবল একটি বৃত্ত আছে। মনে করি, বৃত্তটি $AD$ রেখাংশকে $E$ বিন্দুতে ছেদ করে। $C$, $E$ যোগ করি।
প্রমাণ : অঙ্কন অনুসারে $ABCE$ বৃত্তস্থ চতুর্ভুজ।
সুতরাং $\angle ABC + \angle AEC=$ দুই সমকোণ [বৃত্তে অন্তর্লিখিত চতুর্ভুজের যেকোনো দুইটি বিপরীত কোণের সমষ্টি দুই সমকোণ]
কিন্তু $\angle ABC + \angle ADC=$ দুই সমকোণ [দেওয়া আছে]
$\therefore \angle AEC = \angle ADC$
কিন্তু তা অসম্ভব। কারণ চিত্রে $\triangle CED$ এর বহিঃস্থ $\angle AEC >$ বিপরীত অন্তঃস্থ $\angle ADC$
সুতরাং $E$ এবং $D$ বিন্দুদ্বয় ভিন্ন হতে পারে না। $E$ বিন্দু অবশ্যই $D$ বিন্দুর সাথে মিলে যাবে।
অতএব, $A$, $B$, $C$, $D$ বিন্দু চারটি সমবৃত্ত। (প্রমাণিত)
⚡ Trending Posts
Leave a Comment (Text or Voice)
Comments (0)