উপপাদ্য : বৃত্তের একই চাপের ওপর দণ্ডায়মান কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ।
| History | 📡 Page Views |
|---|---|
|
Published 11-Dec-2025 | 01:53 AM |
Total View 69 |
|
Last Updated 31-Dec-2025 | 07:33 PM |
Today View 0 |
বৃত্তের একই চাপের ওপর দণ্ডায়মান কেন্দ্রস্থ কোণ বৃত্তস্থ কোণের দ্বিগুণ।
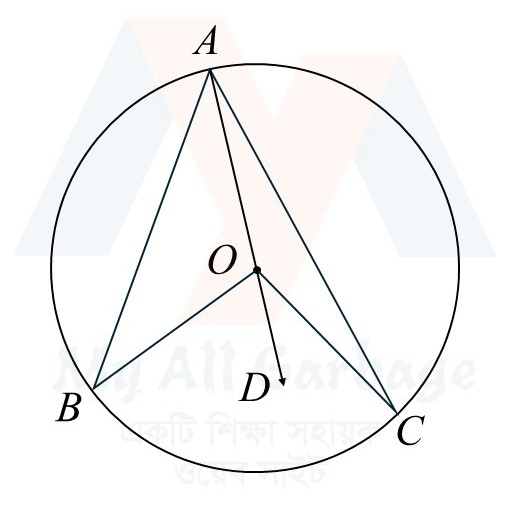
মনে করি, $AC$ রেখাংশ কেন্দ্রগামী নয়। এ ক্ষেত্রে $A$ বিন্দু দিয়ে কেন্দ্রগামী রেখাংশ $AD$ আঁকি।
অঙ্কন : মনে করি, $AC$ রেখাংশ কেন্দ্রগামী নয়। এ ক্ষেত্রে $A$ বিন্দু দিয়ে কেন্দ্রগামী রেখাংশ $AD$ আঁকি।
প্রমাণ :
ধাপ-১: $\triangle AOB$ এর বহিঃস্থ কোণ $\angle BOD = \angle BAO + \angle ABO$ [$\therefore$ বহিঃস্থ কোণ অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান]
ধাপ-২: $\triangle AOB$ এ $OA=OB$ [$\therefore$ একই বৃত্তের ব্যাসার্ধ]
অতএব, $\angle BAO = \angle ABO$ [$\therefore$ সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণ দুইটি সমান]
ধাপ-৩: ধাপ-(১) ও (২) থেকে $\angle BOD = 2\angle BAO$
ধাপ-৪: একইভাবে $\triangle AOC$ থেকে $\angle COD = 2 \angle CAO$
ধাপ-৫: ধাপ-(৩) ও (৪) থেক
$\angle BOD + \angle COD = 2\angle BAO + 2\angle CAO$ [যোগ করে]
অর্থাৎ $\angle BOC = 2\angle BAC$ [প্রমাণিত]

Leave a Comment (Text or Voice)
Comments (0)