উপপাদ্য : বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে বৃত্তে দুইটি স্পর্শক টানলে, ঐ বিন্দু থেকে স্পর্শ বিন্দুদ্বয়ের দূরত্ব সমান।
| History | 📡 Page Views |
|---|---|
|
Published 28-Nov-2025 | 07:35 PM |
Total View 36 |
|
Last Updated 31-Dec-2025 | 07:41 PM |
Today View 0 |
বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে বৃত্তে দুইটি স্পর্শক টানলে, ঐ বিন্দু থেকে স্পর্শ বিন্দুদ্বয়ের দূরত্ব সমান।
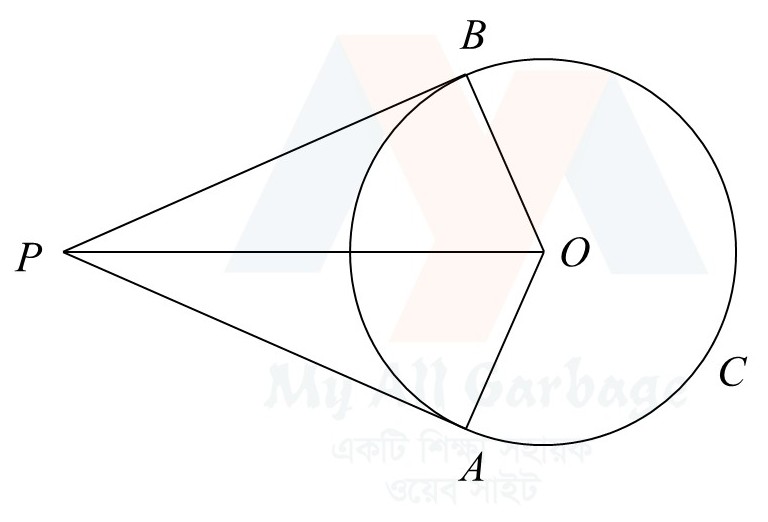
মনে করি, $O$ কেন্দ্রবিশিষ্ট $ABC$ বৃত্তের $P$ একটি বহিঃস্থ বিন্দু এবং $PA$ ও $PB$ রেখাংশদ্বয় বৃত্তের $A$ ও $B$ বিন্দুতে দুইটি স্পর্শক। প্রমাণ করতে হবে যে, $PA=PB$
অঙ্কন : $O$, $A$; $O$, $B$ এবং $O$, $P$ যোগ করি।
প্রমাণ :
ধাপ ১ - যেহেতু $PA$ স্পর্শক এবং $OA$ স্পর্শবিন্দুগামী ব্যাসার্ধ, যেহেতু $PA \perp OA$
$\therefore$ $\angle PAO=$ এক সমকোণ। [$\because$ স্পর্শক স্পর্শবিন্দুগামী ব্যাসার্ধের ওপর লম্ব]
অনুরূপ $\angle PBO=$ এক সমকোণ।
$\therefore$ $\triangle PAO$ এবং $\triangle PBO$ উভয়ই সমকোণী ত্রিভুজ।
ধাপ ২ - এখন, $\triangle PAO$ এবং $\triangle PBO$ সমকোণী ত্রিভুজদ্বয়ে-
অতিভুজ $PO$ $=$ অতিভুজ $PO$
$OA=OB$ [$\because$ একই বৃত্তের ব্যাসার্ধ]
$\therefore$ $\triangle PAO \cong \triangle PBO$ [সমকোণী ত্রিভুজের অতিভুজ-বাহু সর্বসমতা]
সুতরাং, $PA=PB$ (প্রমাণিত)

Leave a Comment (Text or Voice)
Comments (0)