উপপাদ্য : বৃত্তের সকল সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
| History | 📡 Page Views |
|---|---|
|
Published 14-Dec-2025 | 11:43 PM |
Total View 113 |
|
Last Updated 31-Dec-2025 | 07:32 PM |
Today View 0 |
বৃত্তের সকল সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
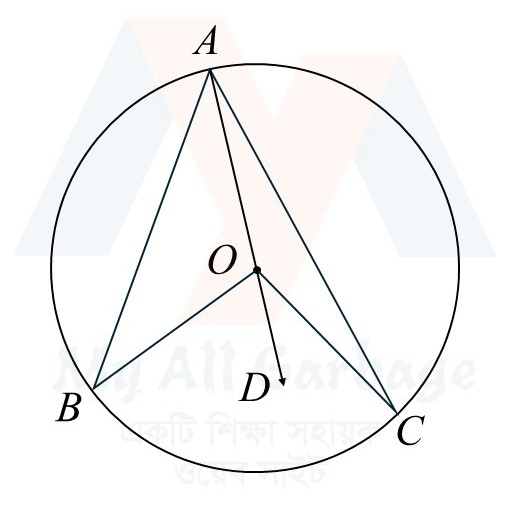
মনে করি, $O$ বৃত্তের কেন্দ্র এবং $AB$ ও $CD$ বৃত্তের দুইটি সমান জ্যা।
প্রমাণ করতে হবে যে, $O$ থেকে $AB$ এবং $CD$ জ্যাদ্বয় সমদূরবর্তী।
অঙ্কন : $O$ থেকে $AB$ এবং $CD$ জ্যা এর উপর যথাক্রমে $OE$ এবং $OF$ লম্ব রেখাংশ আঁকি। $O$, $A$ এবং $O$, $C$ যোগ করি।
প্রমাণ :
ধাপ-১ : $OE \perp AB$ এবং $OF \perp CD$
সুতরাং, $AE=BE$ এবং $CF = DF$ [$\because$ কেন্দ্র থেকে ব্যাস ভিন্ন যেকোনো জ্যা এর উপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে]
$\therefore$ $AE=\frac12 AB$ এবং $CF=\frac12 CD$
ধাপ-২ : কিন্তু $AB=CD$ [ধরে নেয়া]
$\therefore AE = CF$
ধাপ-৩ : এখন $\triangle OAE$ এবং $\triangle OCF$ সমকোণী ত্রিভুজদ্বয়ের মধ্যে
অতিভুজ $OA =$ অতিভুজ $OC$ [উভয়ে একই বৃত্তের ব্যাসার্ধ]
এবং
$AE=CF$ [ধাপ ২]
$\therefore$ $\triangle OAE \cong \triangle OCF$ [সমকোণী ত্রিভুজের অতিভুজ-বাহু সর্বসমতা উপপাদ্য]
$\therefore OE = OF$
ধাপ-৪ : কিন্তু $OE$ এবং $OF$ কেন্দ্র $O$ থেকে যথাক্রমে $AB$ জ্যা এবং $CD$ জ্যা এর দূরত্ব।
সুতরাং, $AB$ এবং $CD$ জ্যাদ্বয় বৃত্তের কেন্দ্র থেকে সমদূরবর্তী। (প্রমাণিত)

Leave a Comment (Text or Voice)
Comments (0)