কোনো নির্দিষ্ট স্থূলকোণী ত্রিভুজের পরিবৃত্ত আঁকতে হবে।
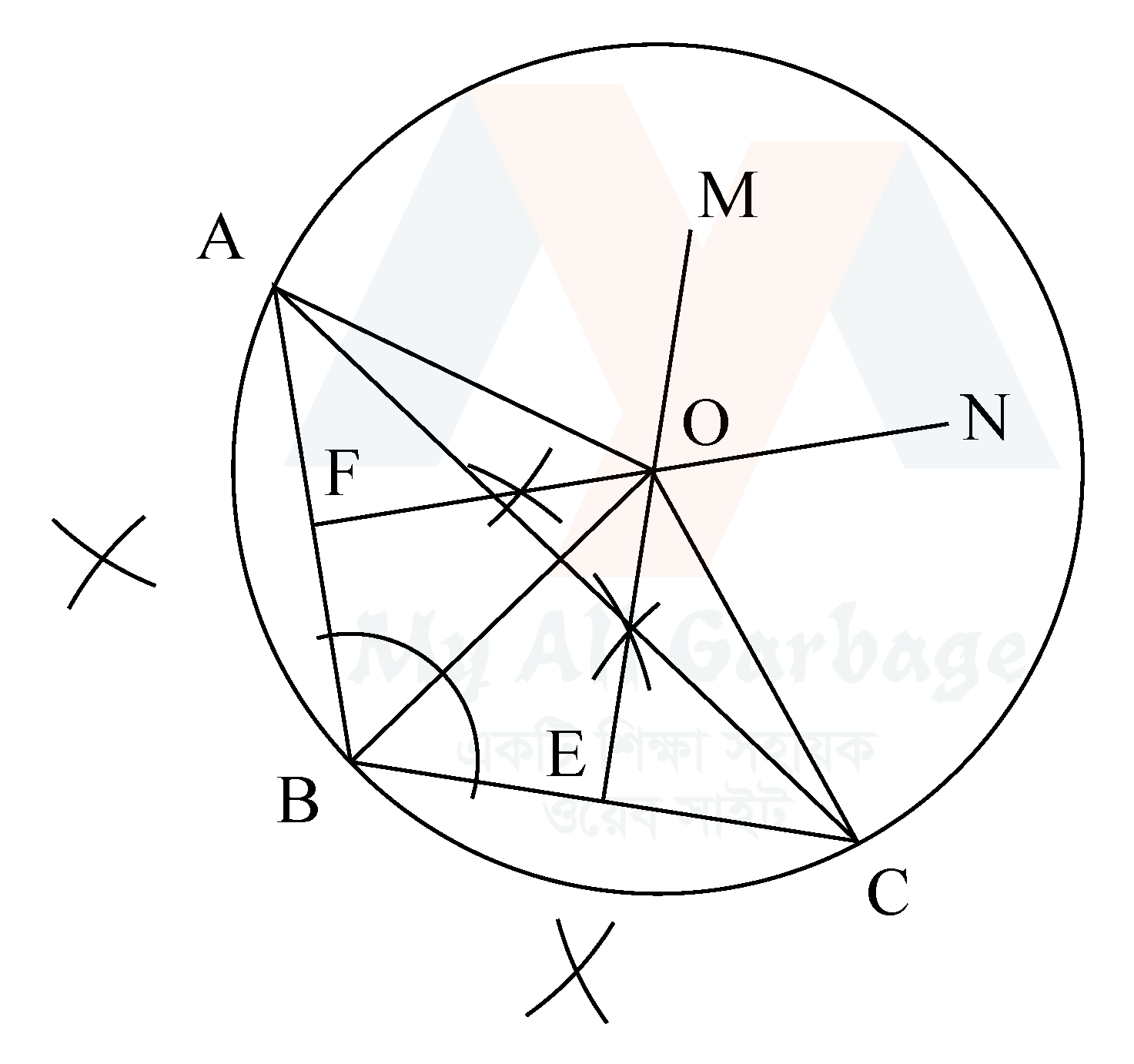
মনে করি, $ABC$ একটি স্থূলকোণী ত্রিভুজ, যার $\angle B$ স্থূলকোণ। এর পরিবৃত্ত আঁকতে হবে। অর্থাৎ, এমন একটি বৃত্ত আঁকতে হবে, যা ত্রিভুজের তিনটি শীর্ষবিন্দু $A$, $B$ ও $C$ বিন্দু দিয়ে যায় বা যার কেন্দ্র $A$, $B$ ও $C$ থেকে সমদূরবর্তী।
- ১. $AB$ ও $BC$ রেখাংশের লম্ব সমদ্বিখণ্ডক যথাক্রমে $FN$ ও $EM$ রেখাংশ আঁকি। মনে করি, তারা পরস্পরকে $O$ বিন্দুতে ছেদ করে।
- ২. $A$, $O$ যোগ করি। $O$ কে কেন্দ্র করে $OA$ এর মান ব্যাসার্ধ নিয়ে একটি বৃত্ত আঁকি।
তাহলে, বৃত্তটি $A$, $B$ ও $C$ বিন্দুগামী হবে এবং এই বৃত্তটিই $\triangle ABC$ এর নির্ণেয় পরিবৃত্ত।
প্রমান : $B$, $O$ ও $C$, $O$ যোগ করি। $O$ বিন্দুটি $AB$ এর লম্বদ্বিখণ্ডক $FN$ এর ওপর অবস্থিত।
$\therefore OA=OB$, একইভাবে $OB=OC$
$\therefore OA=OB=OC$
সুতরাং $O$ কে কেন্দ্র করে $OA$ এর সমান ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্তটি $A$, $B$ ও $C$ বিন্দু তিনটি দিয়ে যাবে বা $OA=OB=OC$ হওয়ায় কেন্দ্র $O$ থেকে $A$, $B$ ও $C$ সমদূরবর্তী। সুতরাং এই বৃত্তটিই $\triangle ABC$ এর পরিবৃত্ত।
আবার, কোনো নির্দিষ্ট সমকোণী ত্রিভুজের পরিবৃত্ত আঁকতে হবে।
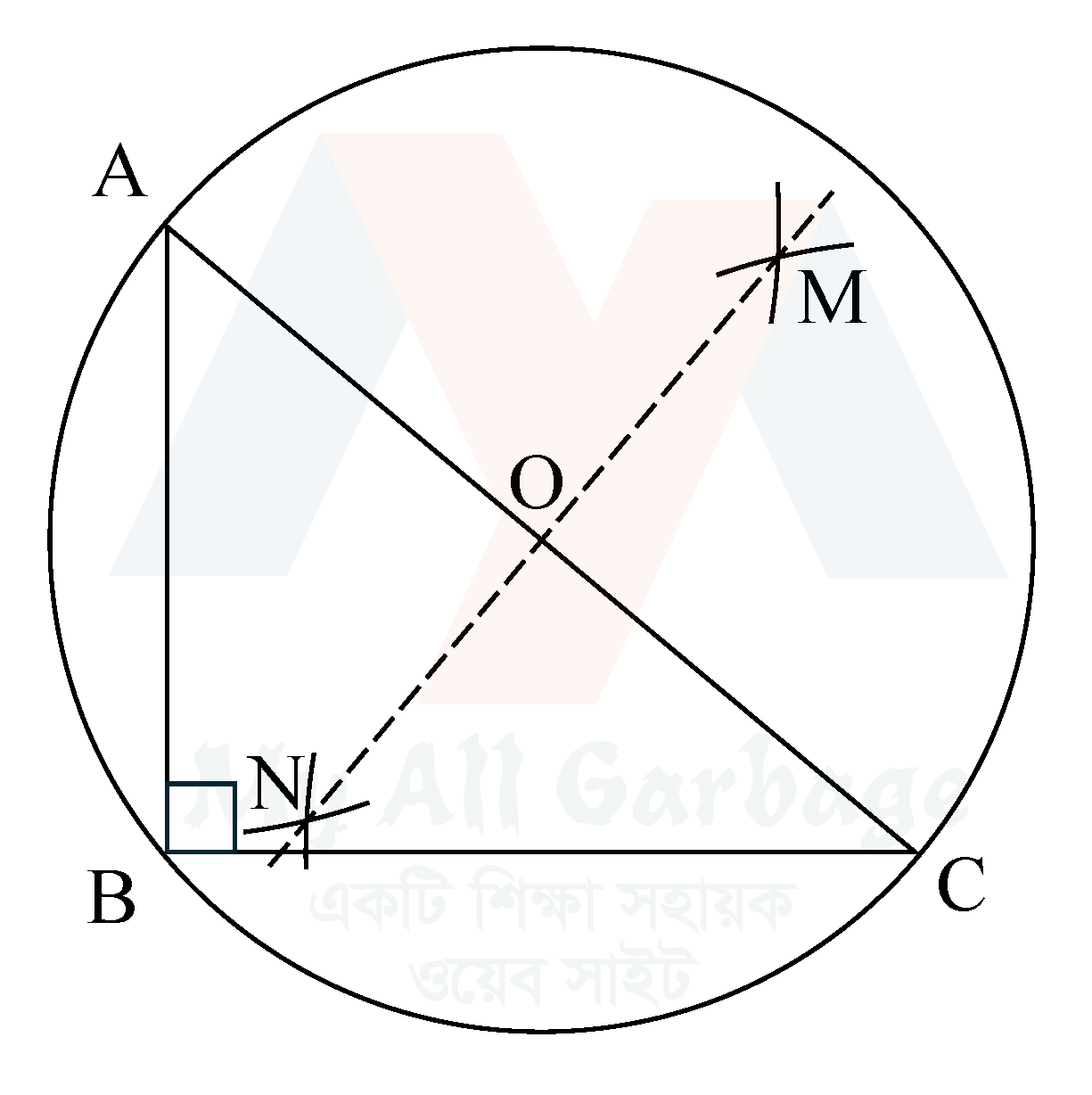
মনে করি, $ABC$ একটি সমকোণী ত্রিভুজ, যার $\angle B$ সমকোণ। এর পরিবৃত্ত আঁকতে হবে। অর্থাৎ, এমন একটি বৃত্ত আঁকতে হবে, যা ত্রিভুজের তিনটি শীর্ষবিন্দু $A$, $B$ ও $C$ বিন্দু দিয়ে যায়।
সমকোণী ত্রিভুজটির অতিভুজ $AC$ এর মধ্যবিন্দু $O$ নির্ণয় করি। $O$ কে কেন্দ্র করে $OA$ এর সমান ব্যসার্ধ নিয়ে একটি বৃত্ত আঁকি, যা $A$, $B$ ও $C$ বিন্দু স্পর্শ করে।
তাহলে, বৃত্তটি $A$, $B$ ও $C$ বিন্দুগামী হবে এবং এই বৃত্তটিই সমকোণী $\triangle ABC$ এর নির্ণেয় পরিবৃত্ত।
প্রমান : যেহেতু অর্ধবৃত্তস্থ কোণ একসমকোণ হয়, তাই উপরের চিত্রানুসারে $AC$ বৃত্তটির ব্যাস এবং বৃস্তটি $A$, $B$ ও $C$ স্পর্শ করেছে তাই বৃত্তটি সমকোণী $\triangle ABC$ এর পরিবৃত্ত।