সম্পাদ্য ৮ : বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে বৃত্তটির স্পর্শক আঁকতে হবে।

বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে বৃত্তটির স্পর্শক আঁকতে হবে।

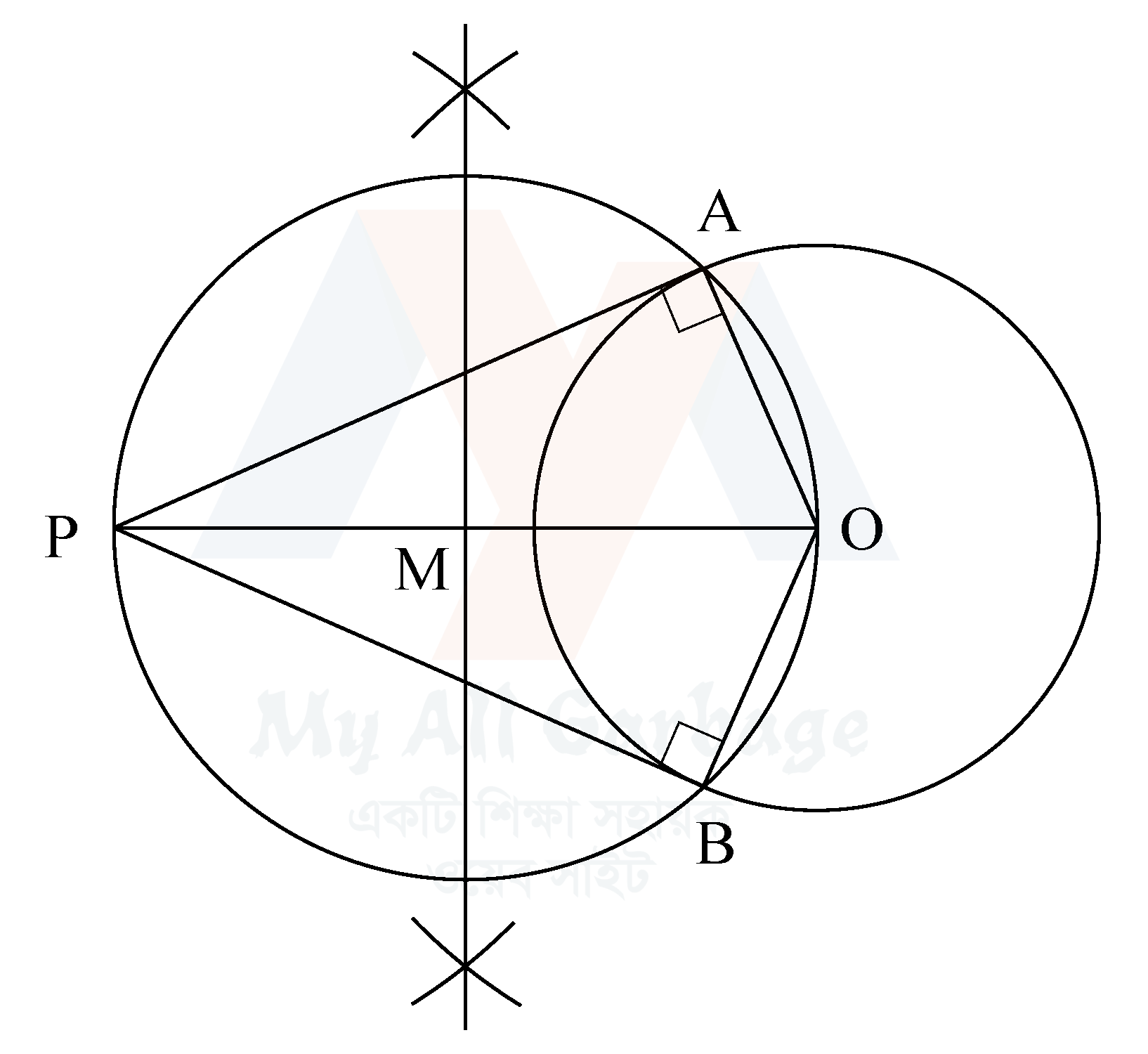
মনে করি, $O$ কেন্দ্রবিশিষ্ট বৃত্তের $P$ একটি বহিঃস্থ বিন্দু। $P$ বিন্দু থেকে ঐ বৃত্তে স্পর্শক আঁকতে হবে।

অঙ্কন :

• ১. $P$, $O$ যোগ করি। $PO$ রেখাংশের মধ্যবিন্দু $M$ নির্ণয় করি।
• ২. এখন $M$ কে কেন্দ্র করে $MO$ এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্ত আঁকি। মনে করি, নতুন অঙ্কিত বৃত্তটি প্রদত্ত বৃত্তকে $A$ ও $B$ বিন্দুতে ছেদ করে।
• ৩. $A$, $P$ ও $B$, $P$ যোগ করি।

তাহলে, $AP$, $BP$ উভয়েই নির্ণেয় স্পর্শক।

প্রমাণ : $A$, $O$ ও $B$, $O$ যোগ করি। $APB$ বৃত্তে $PO$ ব্যাস।

$\angle PAO=$ এক সমকোণ [$\because$ অর্ধবৃত্তস্থ কোণ একসমকোণ]

সুতরাং, $OA$ রেখাংশ $AP$ রেখাংশের ওপর লম্ব। অতএব, $O$ কেন্দ্রিক বৃত্তের $A$ বিন্দুতে $AP$ রেখাংশ একটি স্পর্শক। অনুরূপভাবে, $BP$ রেখাংশও একটি স্পর্শক।