একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান।
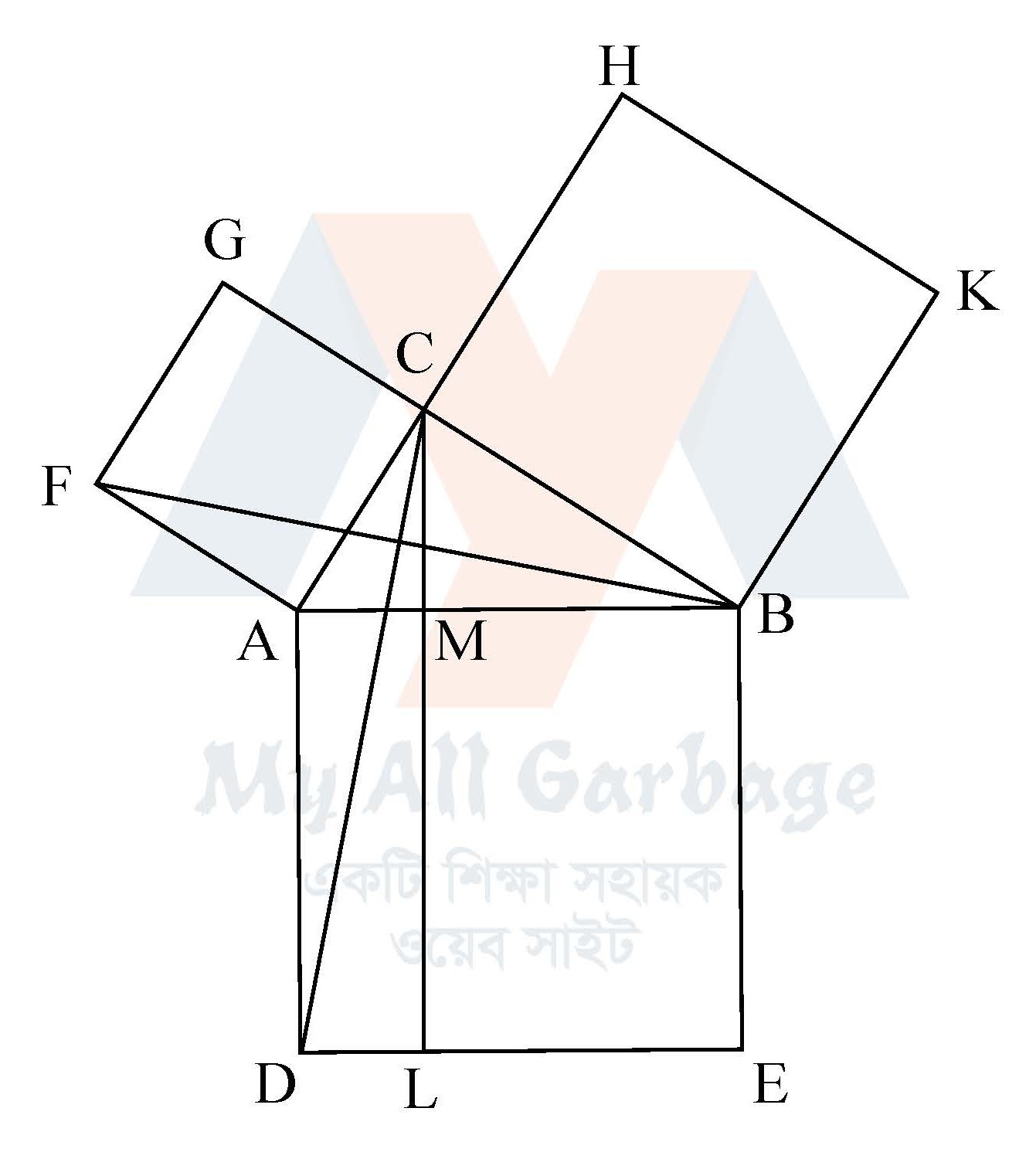
বিশেষ নির্বচন : মনে করি, $ABC$ একটি সমকোণী ত্রিভুজ এর $\angle C$ $=$ এক সমকোণ। সুতরাং $AB$ অতিভুজ। প্রমাণ করতে হবে যে, $AB$ এর উপর অঙ্কিত বর্গক্ষেত্র $=$ $AC$ এর উপর অঙ্কিত বর্গক্ষেত্র $+$ $BC$ এর উপর অঙ্কিত বর্গক্ষেত্র। অর্থাৎ, $AB^2=AC^2+BC^2$
অঙ্কন : $AB$, $AC$ এবং $BC$ বাহুর উপর যথাক্রমে $ABED$, $ACGF$ এবং $BCHK$ বর্গক্ষেত্রদ্বয় অঙ্কন করি। $C$ বিন্দু দিয়ে $AD$ বা, $BE$ রেখার সমান্তরাল $CL$ রেখা আঁকি।
মনে করি, তা $AB$ কে $M$ বিন্দুতে এবং $DE$ কে $L$ বিন্দুতে ছেদ করে।
$C$ ও $D$ এবং $B$ ও $F$ যোগ করি
প্রমাণ : $\angle BAD = \angle CAF$ [প্রত্যেকেই এক সমকোণ]
এখন উভয় পক্ষে $\angle BAC$ যোগ করি।
তাহলে, $\angle BAD+\angle BAC=\angle CAF + \angle BAC$
$\therefore \angle CAD=\angle BAF$ .....($i$)
এখন, $\triangle CAD$ এবং $\triangle BAF$ এ,
$CA=AF$ [$\because$ অঙ্কন অনুসারে $ACFG$ বর্গক্ষেত্র তাই এর প্রত্যেক বাহু সমান]
$AD=AB$ [$\because$ অঙ্কন অনুসারে $ABDE$ বর্গক্ষেত্র তাই এর প্রত্যেক বাহু সমান]
এবং অন্তর্ভুক্ত $\angle CAD=$অন্তর্ভুক্ত $\angle BAF$ [($i$) অনুসারে]
$\therefore \triangle CAD \cong \triangle BAF$ .....($ii$)
Click to see note
যদি দুইটি ত্রিভুজের মধ্যে পরস্পর দুইটি বাহু ও উক্ত বাহুদ্বয়ের অন্তর্ভুক্ত কোণদ্বয় সমান হয়, তবে ত্রিভুজদ্বয় সর্বসম।
যেহেতু $\angle ACB$ এবং $\angle ACG$ এর প্রত্যেকে এক সমকোণ।
$\therefore BCG$ একই সরলরেখা
এখন যেহেতু $\triangle CAD$ এবং আয়তক্ষেত্র $ADLM$ একই ভূমি $AD$ এর উপর এবং $AD$ ও $CL$ সমান্তরাল রেখাদ্বয়ের মধ্যে অবস্থিত, সেহেতু
আয়তক্ষেত্র $ADLM=2(\triangle CAD)$ .....($iii$)
Click to see note
এখানে,
আয়তক্ষত্র $ADLM=$ভূমি$\times$উচ্চতা
এবং
$\triangle CAD$$=$$\frac12$$\times$ভূমি$\times$উচ্চতা
$\therefore 2\triangle CAD$$=$ভূমি$\times$উচ্চতা
উভয় ক্ষেত্রেই মান যেহেতু (ভূমি$\times$উচ্চতা)
তাই, আয়তক্ষেত্র $ADLM=2(\triangle CAD)$
আবার, যেহেতু $\triangle BAF$ এবং বর্গক্ষেত্র $ACGF$ একই ভূমি $AF$ এর উপর এবং $AF$ ও $BG$ সমান্তরাল রেখাদ্বয়ের মধ্যে অবস্থিত, সেহেতু
বর্গক্ষেত্র $ACGF=2(\triangle BAF)=2(\triangle CAD)$ [($ii$) অনুসারে] .....($iv$)
($iii$) ও ($iv$) নং সমীকরণ বিবেচনা করে পাই,
আয়তক্ষেত্র $ADLM$ $=$ বর্গক্ষেত্র $ACGF$ .....($v$)
অনুরূপভাবে, $C$, $E$ ও $A$, $K$ যোগ করে প্রমাণ করা যায় যে,
আয়তক্ষেত্র $BELM$ $=$ বর্গক্ষেত্র $BCHK$ .....($vi$)
($v$) ও ($vi$) নং সমীকরণ যোগ করে পাওয়া যায়,
আয়তক্ষেত্র $ADLM$ $+$ আয়তক্ষেত্র $BELM$ $=$ বর্গক্ষেত্র $ACGF$ $+$ বর্গক্ষেত্র $BCHK$
বা, বর্গক্ষেত্র $ADEB$ $=$ বর্গক্ষেত্র $ACGF$ $+$ বর্গক্ষেত্র $BCHK$
অর্থাৎ, $AB$ এর উপর অঙ্কিত বর্গক্ষেত্র $=$ $AC$ এর উপর অঙ্কিত বর্গক্ষেত্র $+$ $BC$ এর উপর অঙ্কিত বর্গক্ষেত্র।
$\therefore$ $AB^2=AC^2+BC^2$ [প্রমাণিত]
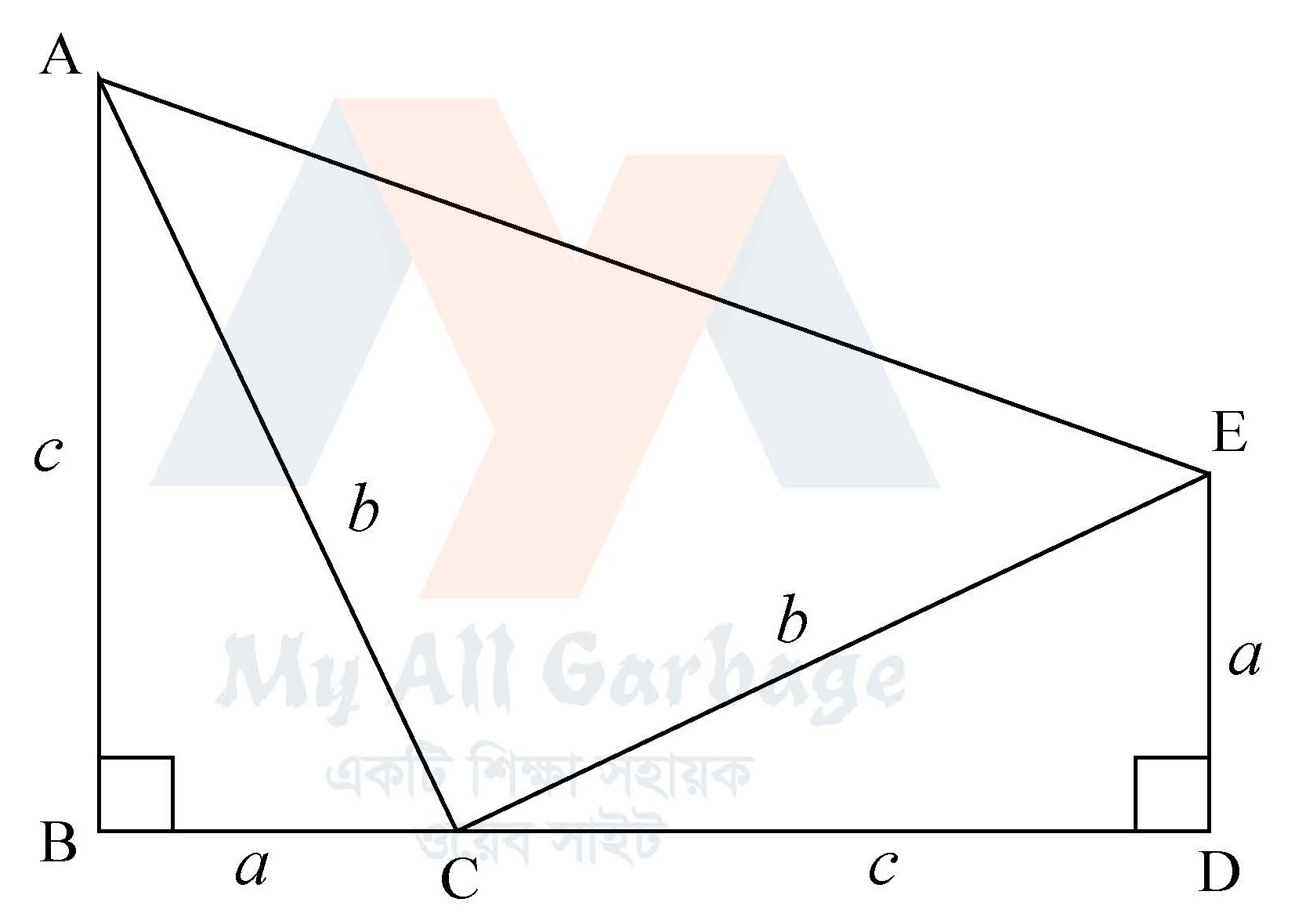
বিশেষ নির্বচন : মনে করি, $ABC$ সমকোণী ত্রিভুজের $\angle B=90^\circ$ অতিভুজ $AC=b$, $AB=c$ ও $BC=a$
প্রমাণ করতে হবে যে, $AC^2=AB^2+BC^2$, অর্থাৎ $b^2=c^2+a^2$
অঙ্কন : $BC$ কে $D$ পর্যন্ত বর্ধিত করি, যেন $CD=AB=c$ হয়। $D$ বিন্দুতে বর্ধিত $BC$ এর উপর $DE$ লম্ব আঁকি, যেন $DE=BC=a$ হয়। $C$, $E$ ও $A$, $E$ যোগ করি।
প্রমাণ :
(Step-1)
$\triangle ABC$ ও $\triangle CDE$ এ
$AB=CD=c$, [অঙ্কনানুসারে]
$BC=DE=a$ [অঙ্কনানুসারে]
এবং অন্তর্ভুক্ত $\angle ABC$ $=$ অন্তর্ভুক্ত $\angle CDE$ [প্রত্যেকেই সমকোণ]
$\therefore \triangle ABC \cong \triangle CDE$
Click to see note
যদি দুইটি ত্রিভুজের মধ্যে পরস্পর দুইটি বাহু ও উক্ত বাহুদ্বয়ের অন্তর্ভুক্ত কোণদ্বয় সমান হয়, তবে ত্রিভুজদ্বয় সর্বসম।
$\therefore$$AC=CE=b$ এবং $\angle BAC = \angle ECD$
(Step-2)
আবার, $AB \perp BD$ এবং $ED \perp BD$ হওয়ায়, $AB \parallel ED$
সুতরাং, $ABDE$ একটি ট্রাপিজিয়াম।
(Step-3)
তদুপরি, $\angle ACB$$+$$\angle BAC$$=$$\angle ACB$$\angle ECD$$=$এক সমকোণ।
$\therefore$ $\angle ACE$$=$এক সমকোণ।
$\therefore$ $\triangle ACE$$=$সমকোণী ত্রিভুজ।
Click to see note
আমরা জানি,
- ট্রাপিজিয়াম ক্ষেত্রের ক্ষেত্রফল$=$$\frac12$$\times$সমান্তরাল বাহুদ্বয়ের মধ্যবর্তী দূরত্ব$\times$সমান্তরাল বাহুদ্বয়ের যোগফল
- ত্রিভুজ ক্ষেত্রের ক্ষেত্রফল$=$$\frac12$$\times$ভূমি$\times$উচ্চতা
এখন, $ABDE$ ট্রাপিজিয়ামক্ষেত্রের ক্ষেত্রফল $=$ $\triangle ABC$ এর ক্ষেত্রফল $+$ $\triangle CDE$ এর ক্ষেত্রফল $+$ $\triangle ACE$ এর ক্ষেত্রফল
বা, $\frac12 BD(AB+DE)=$$\frac12 ac + \frac12 ac + \frac12 b^2$
বা, $\frac12 (BC+CD)(AB+DE)=$$\frac 12(2ac+b^2)$
বা, $(a+c)(a+c)=2ac+b^2$ [উভয় পক্ষকে $2$ দ্বারা গুণ করে]
বা, $(a+c)^2=2ac+b^2$
বা, $a^2+2ac+c^2=2ac+b^2$
$\therefore a^2+c^2=b^2$ [প্রমাণিত]
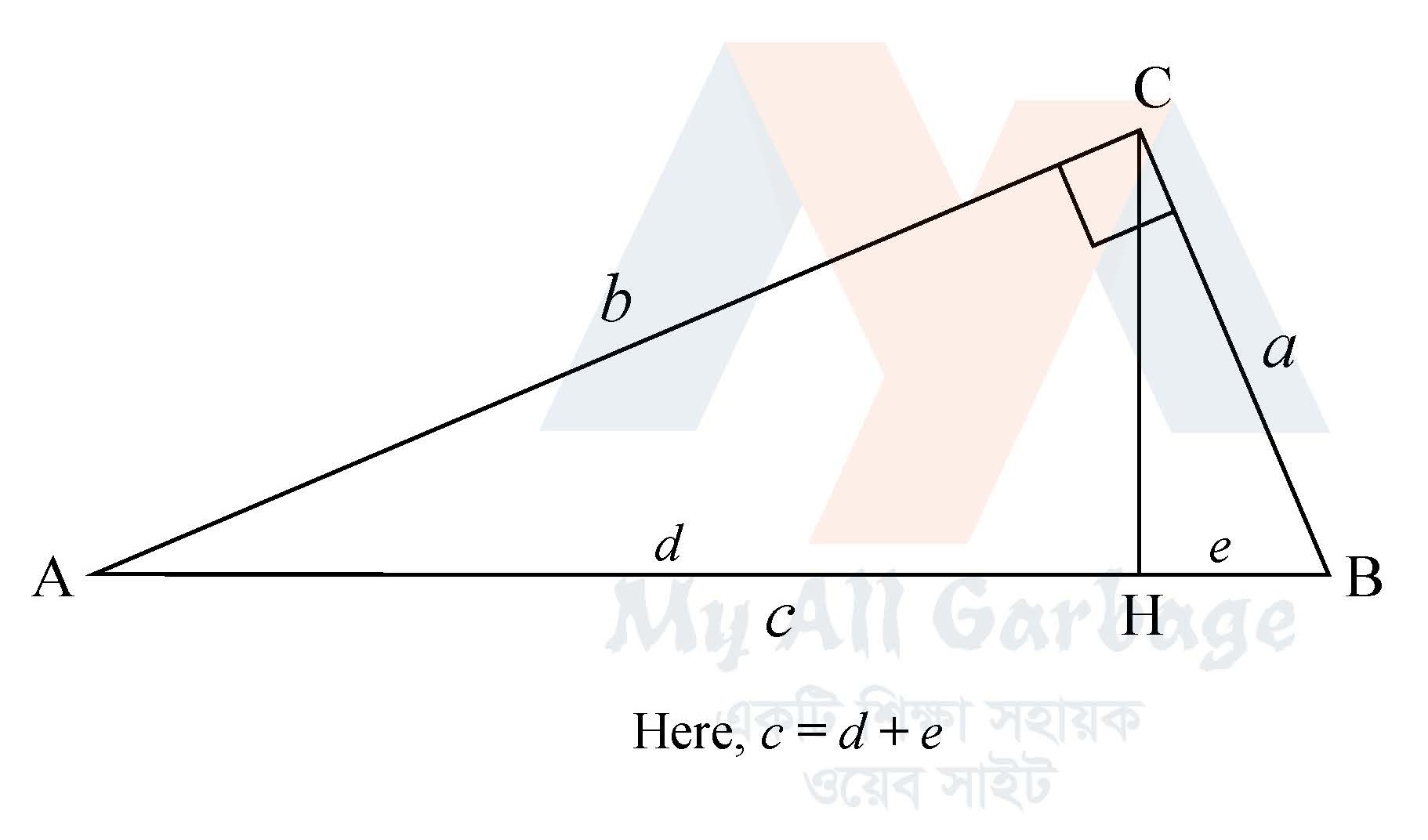
বিশেষ নির্বচন : মনে করি, $ABC$ সমকোণী ত্রিভুজের $\angle C=90^\circ$ অতিভুজ $AB=c$, $BC=a$ ও $AC=b$
প্রমাণ করতে হবে যে, $AB^2=AC^2+BC^2$, অর্থাৎ $c^2=a^2+b^2$
অঙ্কন : $C$ বিন্দু থেকে অতিভুজ $AB$ এর উপর লম্ব $CH$ অঙ্কন করি। $AB$ অতিভুজ $H$ বিন্দুতে $d$ ও $e$ অংশে বিভক্ত হলো।
প্রমাণ :
$\triangle BCH$ ও $\triangle ABC$ এ
$\angle BHC=\angle ACB$ এবং
$\angle CBH=\angle ABC$
$\therefore$$\triangle CBH$ ও $\triangle ABC$ সদৃশ।
সুতরাং $\frac{BC}{AB}=\frac{BH}{BC}$
বা, $\frac{a}{c}=\frac{e}{a}$
$\therefore a^2=ce$ .....($i$)
অনুরূপ ভাবে $\triangle ACH$ ও $\triangle ABC$ সদৃশ।
সুতরাং $\frac{b}{c}=\frac{d}{b}$
$\therefore b^2=cd$ .....($ii$)
($i$) ও ($ii$) নং সমীকরণ যোগ করে পাই,
$a^2+b^2=ce + cd$
বা, $a^2+b^2=c (e + d)$
বা, $a^2+b^2=c \times c$ [$\because c=e+d$]
$\therefore a^2+b^2=c^2$ [প্রমাণিত]
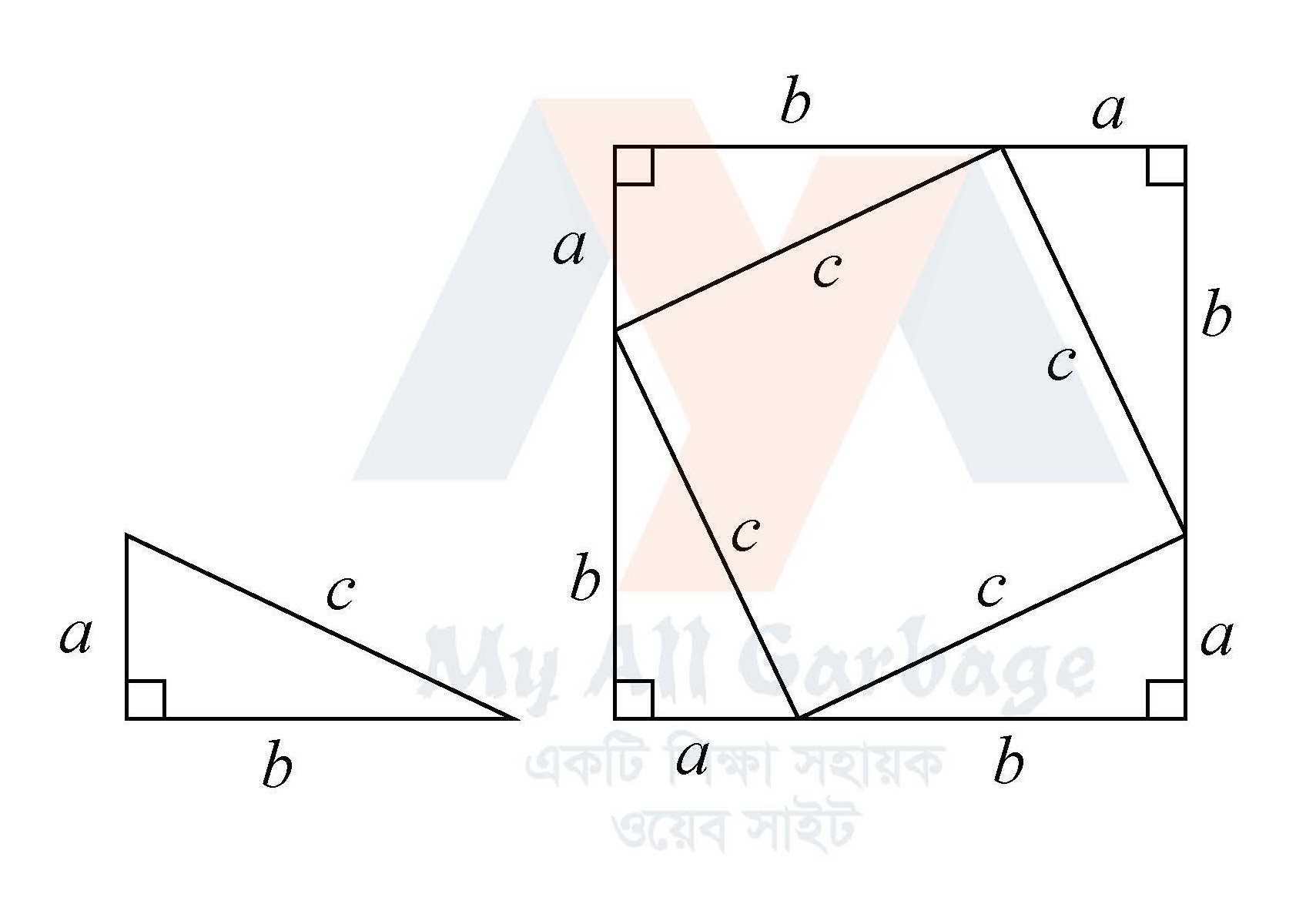
বিশেষ নির্বচন : মনে করি, $ABC$ সমকোণী ত্রিভুজের অতিভুজ $c$ এবং অপর দুই বাহু যথাক্রমে $a$, $b$
প্রমাণ করতে হবে যে, $c^2=a^2+b^2$
অঙ্কন : প্রদত্ত ত্রিভুজের সমান করে চারটি ত্রিভুজ চিত্রে প্রদর্শিত উপায়ে আঁকি।
প্রমান :
অঙ্কিত বড় ক্ষেত্রটি বর্গক্ষেত্র। কারণ, বাহুগুলোর প্রত্যেকটির দৈর্ঘ্য $a+b$ এবং কোণগুলো সমকোণ।
সুতরাং এর ক্ষেত্রফল $(a+b)^2$
বড় বর্গক্ষেত্রের অভ্যন্তরে ছেট ক্ষেত্রটিও একটি বর্গক্ষেত্র। কারণ বাহুগুলোর প্রত্যেকটির দৈর্ঘ্য $c$।
তাহলে এর ক্ষেত্রফল $c^2$
অঙ্কনানুসারে, বড় বর্গক্ষেত্রের ক্ষেত্রফল, চারটি ত্রিভুজক্ষেত্র ও ছোট বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান।
অর্থাৎ,
$(a+b)^2=4\left(\frac{1}{2}ab\right)+c^2$
বা, $a^2+2ab+b^2=2ab+c^2$
বা, $a^2+2ab+b^2-2ab=c^2$
$\therefore a^2+b^2=c^2$ [প্রমাণিত]
যদি কোনো ত্রিভুজের একটি বাহুর উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান হয়, তবে শেষোক্ত বাহুদ্বয়ের অন্তর্ভুক্ত কোণটি সমকোণ হবে।
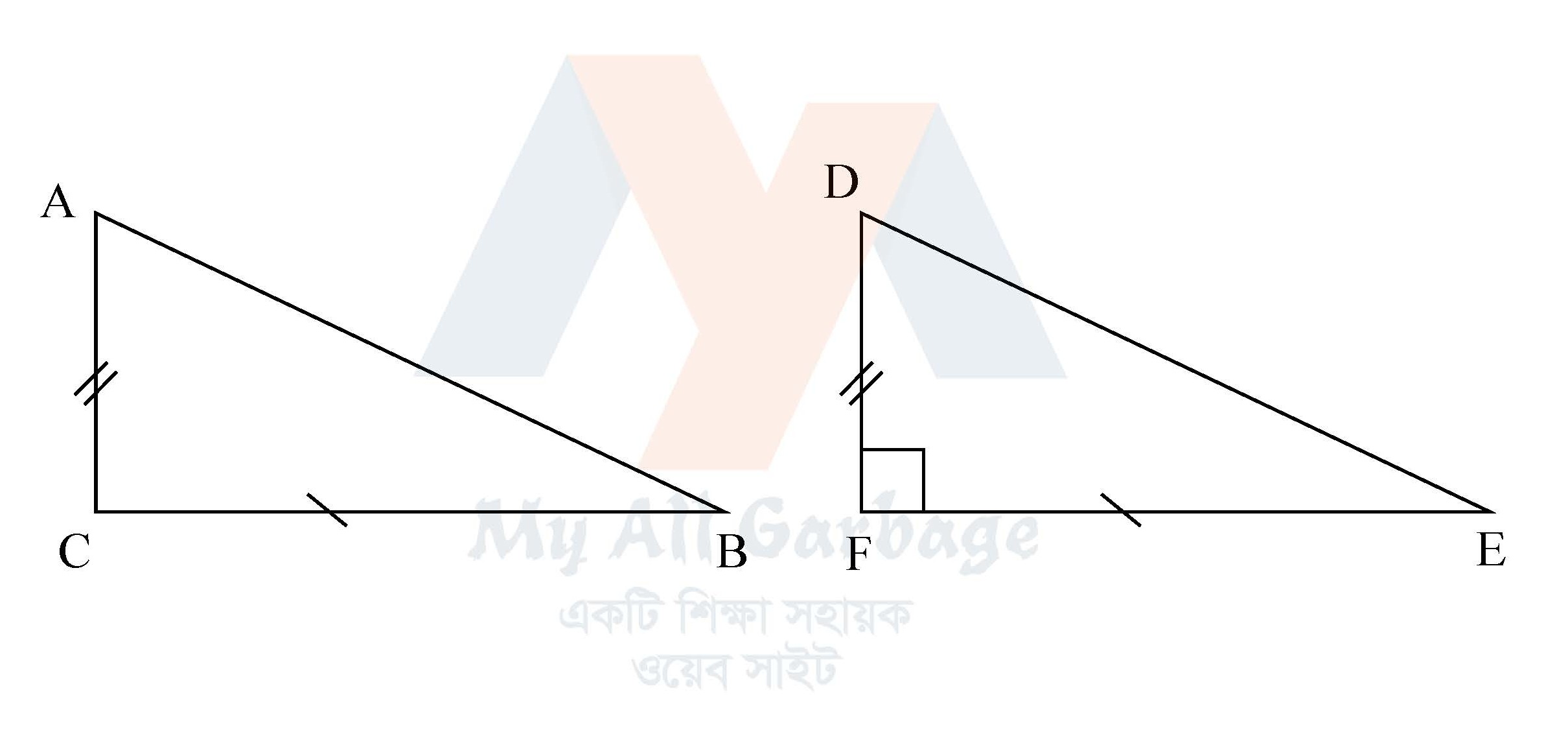
বিশেষ নির্বচন : মনে করি, $ABC$ সমকোণী ত্রিভুজের $AB^2=AC^2+BC^2$
প্রমাণ করতে হবে যে, $\angle C$$=$এক সমকোণ।
অঙ্কন : এমন একটি ত্রিভুজ $DEF$ আঁকি, যেন $\angle F$$=$এক সমকোণ এবং $EF=BC$ এবং $DF=AC$ হয়।
প্রমান :
$DE^2=EF^2+DF^2$ [কারণ $\triangle DEF$ এ $\angle F$ এক সমকোণ]
বা, $DE^2=BC^2+AC^2$ [অঙ্কনানুসারে]
বা, $DE^2=AB^2$ [দেওয়া আছে]
$\therefore DE=AB$ [বর্গমূল করে] .....($i$)
এখন $\triangle ABC$ ও $\triangle DEF$ এ
$BC=EF$, $AC=DF$ [অঙ্কনানুসারে]
$DE=AB$ [($i$) অনুসারে]
$\therefore \triangle ABC \cong \triangle DEF$
Click to see note
যদি দুইটি ত্রিভুজের সবগুলো বাহু অপর ত্রিভুজের সবগুলো বাহুর সমান হয়, তবে ত্রিভুজদ্বয় সর্বসম।
সুতরাং $\angle F=\angle C$
অর্থাৎ $\angle C$$=$এক সমকোণ। [প্রমাণিত]