সম্পাদ্য ১১ : কোনো নির্দিষ্ট ত্রিভুজের বহির্বৃত্ত আঁকতে হবে।
| History | 📡 Page Views |
|---|---|
| Published 10-Oct-2025 | 03:49:00 PM |
Total View 175 |
| Last Updated 31-Dec-2025 | 07:45:14 PM |
Today View 0 |
কোনো নির্দিষ্ট ত্রিভুজের বহির্বৃত্ত আঁকতে হবে।
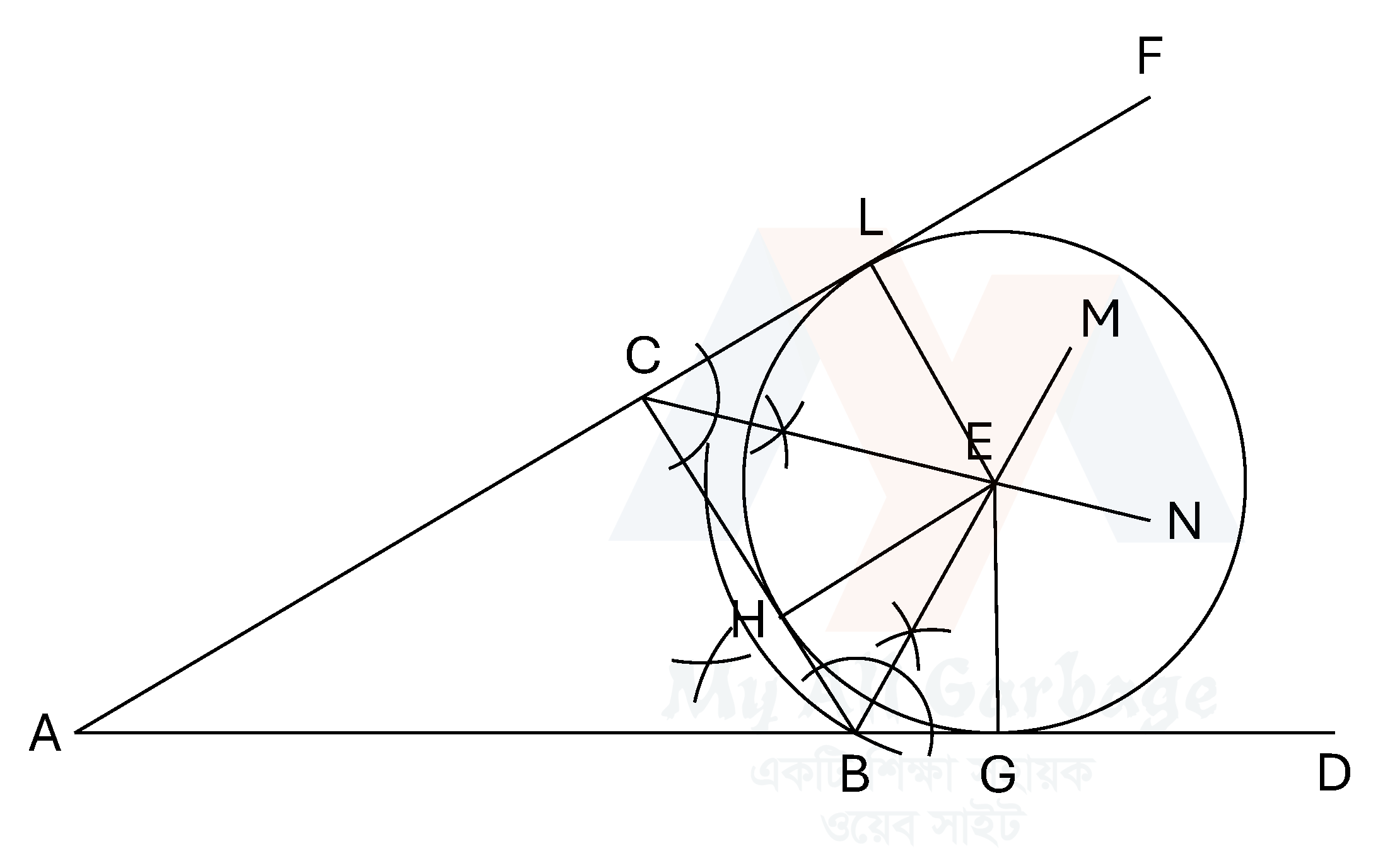
মনে করি, $ABC$ একটি ত্রিভুজ। এর বহির্বৃত্ত আঁকতে হবে। অর্থাৎ, এমন একটি বৃত্ত আঁকতে হবে, যা ত্রিভুজের একটি বাহুকে এবং অপর দুই বাহুর বর্ধিতাংশকে স্পর্শ করে।
অঙ্কন : $AB$ ও $AC$ বাহুদ্বয়কে যথাক্রমে $D$ ও $F$ পর্যন্ত বর্ধিত করি। $\angle DBC$ ও $\angle FCB$ এর সদ্বিখণ্ডক $BM$ ও $CN$ আঁকি।
মনে করি, $E$ এদের ছেদবিন্দু। $E$ থেকে $BC$ এর ওপর $EH$ লম্ব আঁকি এবং মনে করি তা $BC$ কে $H$ বিন্দুতে ছেদ করে। $E$ কে কেন্দ্র করে $EH$ এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্ত আঁকি।
তাহলে, এই বৃত্তটিই নির্ণেয় বহির্বৃত্ত।
প্রমাণ : $E$ থেকে $BD$ ও $CF$ রেখাংশের ওপর যথাক্রমে $EG$ ও $EL$ লম্ব টানি। মনে করি, লম্বদ্বয় $BD$ ও $CF$ রেখাংশদ্বয়কে যথাক্রমে $G$ ও $L$ বিন্দুতে ছেদ করে।
$E$ বিন্দুটি $\angle DBC$ এর দ্বিখণ্ডকের ওপর অবস্থিত $\therefore EH=EG$
অনুরূপভাবে, $E$ বিন্দুটি $\angle FCB$ এর দ্বিখণ্ডকের ওপর অবস্থিত বলে $EH=EL$
$\therefore EH=EG=EL$
সুতরাং $E$ কে কেন্দ্র করে $EL$ এর সমান ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্ত $H$, $G$ এবং $L$ বিন্দু নিয়ে যাবে।
আবার, $EH$, $EG$ ও $EL$ এর প্রান্তবিন্দুতে যথাক্রমে $BC$, $BD$ ও $CF$ রেখাংশ তিনটি লম্ব।
সুতরাং বৃত্তটি রেখাংশ তিনটিকে যথাক্রমে $H$, $G$ ও $L$ বিন্দু তিনটিতে স্পর্শ করে। অতএব, $HGL$ বৃত্তটিই $\triangle ABC$ এর বহির্বৃত্ত হবে।

Leave a Comment (Text or Voice)
Comments (0)